Este blog contém vários artigos em que se demonstra que a Matemática não é uma ciência isolada, pois permite a conexão a múltiplas atividades do nosso quotidiano. Muitas são as vezes em que à Matemática também se pode chegar por outras vias do nosso dia-a-dia, como seja o mundo do Desporto, da Magia, da Cultura, etc.
Ora, o exemplo que escolhi para esta nova reflexão é-nos proposto por Eric Emmet, publicado em 2000 pela Gedisa Editorial*, numa reimpressão de uma primeira publicação em Castelhano de 1990.
O enunciado, adaptado para língua portuguesa, é o seguinte:
"Quatro equipas de futebol - A, B, C e D - vão jogar entre si uma vez. Após se terem realizado alguns - ou talvez todos - os jogos, pode-se conceber uma tabela como a seguinte, onde aparecem alguns aspetos dos jogos jogados, ganhos, perdidos, empatados, golos marcados, golos sofridos e pontuação" (Emmet, 2000. p. 33):
Complete a tabela na íntegra, sabendo que uma vitória vale dois pontos e um empate vale um ponto.
* - Emmet, E. (2000). Juegos de acertijos enigmaticos. Barcelona: gedisa Editorial.
Do ponto de vista matemático, este problema apela bastante ao raciocínio lógico, pois exige por parte do resolvedor o estabelecer de muitas relações entre as diversas variáveis em causa (número de jogos, resultados dos jogos, vitórias, empates, derrotas e pontuação). Além disto, permite o desenvolvimento da comunicação matemática na justificação das opções a tomar.
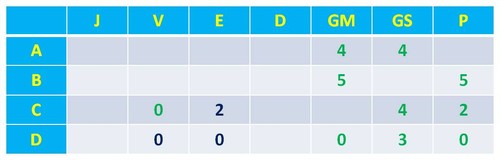
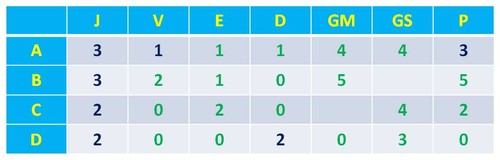
Seria interessante que em contexto de sala de aula os alunos sentissem a força motivacional que a tarefa transporta consigo. Trata-se de algo enigmático, bastante motivador e com importantes pistas para que se possa iniciar o seu processo de resolução. Assim, vejamos que a equipa C ao ter dois pontos e não tendo qualquer vitória, só poderá ter empatado dois jogos. Por sua vez, a equipa D, ao não ter qualquer ponto, não terá conseguido vencer qualquer dos jogos em que esteve envolvida. Logo a tabela poderá começar a ser preenchida tendo em conta estes dois aspetos:
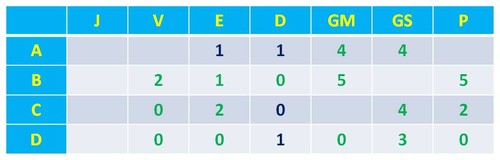
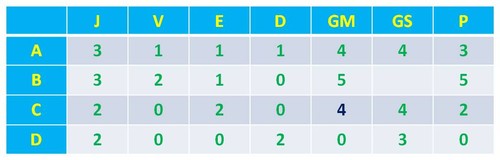
Em continuação o facto de a equipa ter empatado dois jogos, pelos dados da tabela só pode ter sido com as equipas A e B. Resta saber a razão pela qual a equipa B tem 5 pontos. Ora isto só pode ocorrer se esta tiver ganho à equipa D e à equipa A (2 + 2 pontos). Se à pontuação correspondente a estas duas vitórias (4 pontos) adicionarmos um ponto pelo empate com a equipa C, fica justificada a pontuação desta equipa B. Logo, a tabela fica assim:
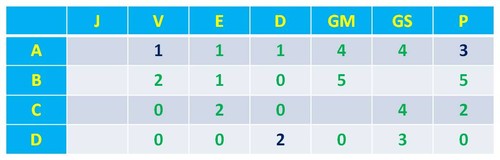
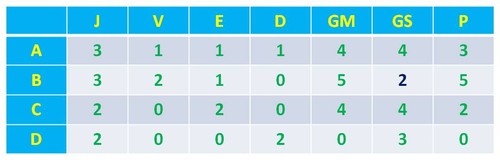
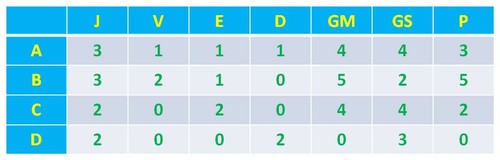
Tendo em conta a tabela anterior, concluímos, pois, que a equipa A tem, pelo menos, um empate com a equipa C e uma derrota com a equipa B. Por sua, vez, a equipa D tem, pelo menos, uma derrota - resultante do jogo com a equipa B. Por último, se a equipa C empatou com as equipas A e B, e a equipa D não tem vitórias, então aquela não tem qualquer derrota. Logo, a tabela fica assim:
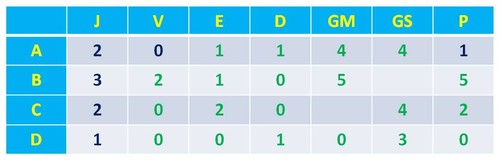
Neste momento nada sabemos sobre o que se passou entre as equipas A e D, pois elas podem ainda não ter jogado entre si (ficando a equipa A só com 1 ponto), ou a equipa A ter já derrotado a equipa D (ficando com 3 pontos). Logo, a partir deste ponto da resolução seria interessante fazer-se um estudo paralelo para estas duas opções acabadas de descrever. Vejamos ambos os cenários:
Cenário 1 - As equipas A e D ainda não terem jogado entre si:
Cenário 2 - A equipa A ter derrotado a equipa D:
Contudo, se com os dados que já temos formos preencher a coluna respeitante aos jogos, constatamos que o cenário 1 não faz sentido:
De facto, nunca a equipa B poderia já ter realizado três jogos e a equipa D só ter realizado um, pois, se assim fosse, não seria possível ocorrer o que se acabou de registar entre a equipa D e a equipa A. Logo, o cenário 1 terá de ser abandonado.
Vejamos como ficaria a tabela preenchendo-se a coluna dos jogos, no caso do cenário 2:
Ora, neste caso, concluímos que as equipas A e B já jogaram com todas as restantes e que ainda faltam defrontar-se as equipas C e D.
Neste momento já só falta descobrir os golos marcados pela equipa C e os golos sofridos pela equipa B. Contudo, uma vez que a equipa C só obteve empates, o número de golos marcados terá de coincidir com o número de golos sofridos:
Por sua vez, o total de golos marcados terá de ser igual ao total de golos sofridos, pelo que a equipa B terá sofrido 2 golos:
De facto, o somatório da coluna dos golos marcados coincide com o somatório da coluna dos golos sofridos: 13 golos. Logo, a tabela final fica com o seguinte aspeto:
Façamos uma extensão ao problema: Será possível prever o resultado de cada jogo realizado?
Em primeiro lugar convirá elencar tudo o que se sabe relativamente a cada equipa:
1 - A equipa D só obteve derrotas e sem qualquer golo marcado. Logo, nenhum dos seus dois adversários com quem já jogou sofreu qualquer golo desta equipa. Por seu turno, quanto aos 3 golos sofridos, o que se sabe é que não foi a equipa C a marcá-los, porque estas duas equipas ainda não jogaram entre si.
2 - Os quatro golos sofridos pela equipa C foram marcados pelas equipas A e B. Por sua vez, os 4 golos que marcou também terão sido a estas duas equipas.
3 - Além dos golos marcados no empate da equipa B com a equipa C, aquela também terá marcado golos nas vitórias com as equipas A e D.
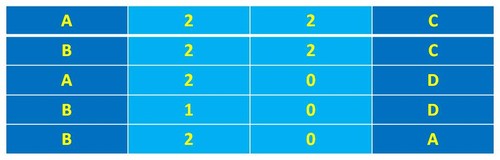
Sendo assim, um cenário possível para esta equipa B seria empatar a 2 golos com a equipa C, ganhar 1 a zero à equipa D e ganhar 2 a zero à equipa A. Se assim for, o outro empate da equipa C, desta vez com a equipa A, também terá de ser 2 a 2. Logo resta-nos a vitória da equipa A sobre a equipa D por 2 a zero:
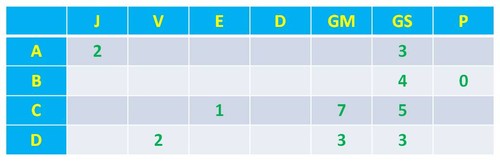
Tendo em conta o mesmo autor, tente resolver um problema semelhante que ele coloca na página 36, cujos dados conhecidos são apenas os da tabela seguinte:





Postar um comentário